| SECT. VII. De corporum Ascensu & Descensu rectilineo. |
|
SECT. VI.
De inventione motuum in Orbibus datis.
Prop. XXX. Prob. XXII.
Corporis in data Trajectoria Parabolica moventis, invenire locum ad tempus assignatum.

Sit S umbilicus & A vertex principalis Parabolæ, sitq; 4AS×M area Parabolica APS, quæ radio SP, vel post excessum corporis de vertice descripta fuit, vel ante appulsum ejus ad verticem describenda est. Innotescit area illa ex tempore ipsi proportionali. Biseca AS in G, erigeq; perpendiculum GH æquale 3M, & circulus centro H, intervallo HS descriptus secabit Parabolam in loco quæsito P. Nam demissa ad axem perpendicu lariPO, est HGq.+GSq.(=HSq.=HPq.=GOq.+.)= GOq.+HGq−2HG×PO+POq. Et deleto utrinq; HGq. fiet GSq.=GOq.−2HG×PO+POq. seu 2HG×PO (=GOq.+POq.−GSq.=AOq.−2GAO+POq.)=AOq.+POq. Pro AOq. scribe AO×, & applicatis terminis omnibus ad 3PO, ductisq; in 2AS, fiet GH×AS(=AO×PO+AS×PO=×PO = ×PO=areæ APO−SPO)= areæ APS. Sed GH erat 3M, & inde HG×AS est 4AS×M. Ergo area APS æqualis est 4AS×M. Q.E.D.
Corol. 1. Hinc GH est ad AS, ut tempus quo corpus descripsit arcum AP ad tempus quo corpus descripsit arcum inter verticem A & perpendiculum ad axem ab umbilico S erectum.
Corol. 2. Et circulo ASP per corpus movens perpetuo transeunte, velocitas puncti H est ad velocitatem quam corpus habuit in vertice A, ut 3 ad 8; adeoq; in ea etiam ratione est linea GH ad lineam rectam quam corpus tempore motus sui ab A ad P, ea cum velocitate quam habuit in vertice A, describere posset.
Corol. 3. Hinc etiam viceversa inveniri potest tempus quo corpus descripsit arcum quemvis assignatum AP. Junge AP & ad medium ejus punctum erige perpendiculum rectæ GH occurrens in H.
Lemma XXVIII.
Nulla extat figura Ovalis cujus area, rectis pro lubitu abscissa, possit per æquationes numero terminorum ac dimensionum finitas generaliter inveniri.
Intra Ovalem detur punctum quodvis, circa quod ceu polum revolvatur perpetuo linea recta, & interea in recta illa exeat punctum mobile de polo, pergatq; semper ea cum velocitate, quæ sit ut rectæ illius intra Ovalem longitudo. Hoc motu punctum illud describet Spiralem gyris infinitis. Jam si area Oualis per finitam æquationem inveniri potest, invenietur etiam per eandem æquationem distantia puncti a polo; quæ huic areæ proportionalis est, adeoq; omnia Spiralis puncta per æquationem finitam inveniri possunt: & propterea rectæ cujusvis positione datæ intersectio cum spirali inveniri etiam potest per æquationem finitam. Atqui recta omnis infinite producta spiralem secat in punctis numero infinitis, & æquatio, qua intersectio aliqua duarum linearum invenitur, exhibet earum intersectiones omnes radicibus totidem, adeoq; ascendit ad tot dimensiones quot sunt intersectiones. Quoniam circuli duo se mutuo secant in punctis duobus, intersectio una non invenitur nisi per æquationem duarum dimensionum, qua intersectio altera etiam inveniatur. Quoniam duarum sectionum Conicarum quatuor esse possunt intersectiones, non potest aliqua earum generaliter inveniri nisi per æquationem quatuor dimensionum, qua omnes simul inveniantur. Nam si intersectiones illæ seorsim quærantur, quoniam eadem est omnium lex & conditio, idem erit calculus in casu unoquoq; & propterea eadem semper conclusio, quæ igitur debet omnes intersectiones simul complecti & indifferenter exhibere. Unde etiam intersectiones Sectionum Conicarum & curvarum tertiæ potestatis, eo quod sex esse possunt, simul prodeunt per æquationes sex dimensionum, & intersectiones duarum curvarum tertiæ potestatis, quia novem esse possunt, simul prodeunt per æquationes dimensionum novem. Id nisi necessario fieret, reducere liceret Problemata omnia Solida ad Plana, & plusquam solida ad solida. Eadem de causa intersectiones binæ rectarum & sectionum Conicarum prodeunt semper per æquationes duarum dimensionum; ternæ rectarum & curvarum tertiæ potestatis per æquationes trium, quaternæ rectarum & curvarum quartæ potestatis per æquationes dimensionum quatuor, & sic in infinitum. Ergo intersectiones numero infinitæ rectarum, propterea quod omnium eadem est lex & idem calculus, requirunt æquationes numero dimensionum & radicum infinitas, quibus omnes possunt simul exhiberi. Si a polo in rectam illam secantem demittatur perpendiculum, & perpendiculum una cum secante revolvatur circa polum, intersectiones spiralis transibunt in se mutuo, quæq; prima erat seu proxima, post unam revolutionem secunda erit, post duas tertia, & sic deinceps: nec interea mutabitur æquatio nisi pro mutata magnitu dine quantitatum per quas positio secantis determinatur. Unde cum quantitates illæ post singulas revolutiones redeunt ad magnitudines primas, æquatio redibit ad formam primam, adeoq; una eademq; exhibebit intersectiones omnes, & propterea radices habebit numero infinitas, quibus omnes exhiberi possunt. Nequit ergo intersectio rectæ & spiralis per æquationem finitam generaliter inveniri, & idcirco nulla extat Ovalis cujus area, rectis imperatis abscissa, possit per talem æquationem generaliter exhiberi.
Eodem argumento, si intervallum poli & puncti, quo spiralis describitur, capiatur Ovalis perimetro abscissæ proportionale, probari potest quod longitudo
perimetri nequit per finitam æquationem generaliter exhiberi.Corollarium.
Hinc area Ellipseos, quæ radio ab umbilico ad corpus mobile ducto describitur, non prodit ex dato tempore, per æquationem finitam; & propterea per descriptionem Curuarum Geometrice rationalium determinari nequit. Curvas Geometrice rationales appello quarum puncta omnia per longitudines æquationibus definitas, id est, per longitudinum rationes complicatas, determinari possunt; cæterasq; (ut Spirales, Quadratrices, Trochoides) Geometrice irrationales. Nam longitudines quæ sunt vel non sunt ut numerus ad numerum (quemadmodum in decimo Elementorum) sunt Arithmetice rationales vel irrationales. Aream igitur Ellipseos tempori proportionalem abscindo per Curvam Geometrice irrationalem ut sequitur.
Prop. XXXI. Prob. XXIII.
Corporis in data Trajectoria Elliptica moventis invenire locum ad tempus assignatum.
Ellipseos APB sit A vertex principalis, S umbilicus, O centrum, sitq; P corporis locus inveniendus. Produc OA ad G ut sit OG ad OA ut OA ad OS. Erige perpendiculum GH, centroq; O & intervallo OG describe circulum EFG, & super regula GH, ceu fundo, progrediatur rota GEF revolvendo circa axem suum, & interea puncto suo A describendo Trochoidem ALI. Quo facto, cape GK in ratione ad rotæ perimetrum GEFG, ut est tempus quo corpus progrediendo ab A descripsit arcum AP, ad tempus revolutionis unius in Ellipsi. Erigatur perpendiculum KL occurrens Trochoidi in L, & acta LP ipsi KG parallela occurret Ellipsi in corporis loco quæsito P.

Nam centro O intervallo OA describatur semicirculus AQB, & arcui AQ occurrat LP producta in Q, junganturq; SQ, OQ. Arcui EF G occurrat OQ in F, &in eandem OQ demittatur perpendiculum SR. Area APS est ut area AQS, id est, ut differentia inter sectorem OQA & triangulum OQS, sive ut differentia rectangulorum Q×AQ & OQ×SR, hoc est, ob datam OQ, ut differentia inter arcum AQ & rectam SR, adeoq; (ob æqualitatem rationum SR ad sinum arcus AQ, OS ad OA, OA ad OG, AQ ad GF, & divisim AQ−SR ad GF−sin.arc.AQ) ut GK differentia inter arcum GF & sinum arcus AQ.
Q.E.D.Scholium.
Cæterum ob difficultatem describendi hanc curvam præstat constructiones vero proximas in praxi Mechanica adhibere. Ellipseos cujusvis APB sit AB axis major, O centrum, S umbilicus, OD semiaxis minor, & AK dimidium lateris recti. Secetur AS in G, ut sit AG ad AS ut BO ad BS; & quæratur longitudo L,quæsitad1 2 GK ut est AO quad. ad rectangulum AS×OD. Bisecetur OG in C, centroq; C & intervallo CG describatur semicirculus GFO. Deniq; capiatur angulus GCF in ea ratione ad angulos quatuor rectos, quam habet tempus datum, quo corpus descripsit arcum quæsitum AP, ad tempus periodicum seu revolutionis unius in Ellipsi: Ad AO demittatur normalis FE, & producatur eadem versus F ad usq; N, ut sit EN ad longitudinem L, ut anguli illius sinus EF ad radium CF; centroq; N & intervallo AN descriptus circulus secabit Ellipsin in corporis loco quæsito P quam proxime.
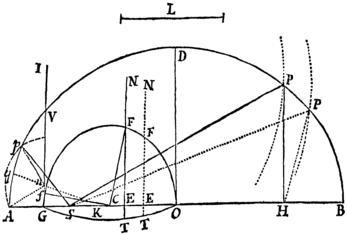
Nam completo dimidio temporis periodici, corpus P semper reperietur in Apside summa B, & completo altero temporis dimidio, redibit ad Apsidem imam, ut oportet. Ubi vero proxime abest ab Apsidibus, ratio prima nascentium sectorum ASP, GCF, & ratio ultima evanescentium BSP & OCF, eadem est rationi Ellipseos totius ad circulum totum. Nam punctis P, F & N incidentibus in loca p, f & n axi AB quam proximis; ob æquales An, pn, recta nq, quæ ad arcum Ap perpendicularis est, adeoq; concurrit cum axe in puncto K, bisecat arcum Ap. Proinde est Ap ad Gn ut AK ad GK, & Ap ad Gn ut 2AK ad GK. Est & Gn ad Gf ut EN ad EF, seu L ad CF, id est, ut ad CF, seu GK×AOq. ad 2AS×OD×CF, & ex æquo Ap ad Gf ut 2AK ad GK+GK×AOq. ad 2AS×OD×CF,id est, ut AK×AOq. ad AS×OD×CF, hoc est, ob æqualia AK×AO×ODq. ut AO×OD ad AS×CF. Proinde Ap× AS est ad Gf×GC ut AO×OD×AS ad AS×CF×GC, seu AO×OD ad CGq. id est, sector nascens ASp ad sectorem nascentem GCf ut AO×OD ad CGq. & propterea ut area Ellipseos totius ad aream circuli totius. Q. E. D. Argumento prolixiore probari potest analogia ultima in Sectoribus evanescentibus BSP, OCF: ideoq; locus puncti P prope Apsides satis accurate inventus est. In quadraturis error quasi quingentesimæ partis areæ Ellipseos totius vel paulo major obvenire solet: qui tamen propemodum evanescet per ulteriorem Constructionem sequentem.
Per puncta G, O, duc arcum circularem GTO justæ magnitudinis; dein produc EF hinc inde ad T & N ut sit EN ad FT ut L ad CF; centroq; N & intervallo AN describe circulum qui secet Ellipsin in P, ut supra. Arcus autem GTO determinabitur quærendo ejus punctum aliquod T; quod constructionem in illo casu accuratam reddet.
Si Ellipseos latus transversum multo majus sit quam latus rectum, & motus corporis prope verticem Ellipseos desideretur, (qui casus in Theoria Cometarum incidit,) educere licet e puncto G rectam GI axi AB perpendicularem, & in ea ratione ad GK quam habet area AVPS ad rectangulum AK×AS; dein centro I & intervallo AI circulum describere. Hic enim secabit Ellipsim in corporis loco quæsito P quamproxime. Et eadem constructione (mutatis mutandis) conficitur Problema in Hyperbola. Hæ autem constructiones demonstrantur ut supra, & si Figura (vertice ulteriore B in infinitum abeunte) vertatur in Parabolam, migrant in accuratam illam constructionem Problematis XXII.

Si quando locus ille P accuratius determinandus sit, inveniatur tum angulus quidam B, qui sit ad angulum graduum 57,29578 quem arcus radio æqualis subtendit, ut est umbilicorum distantia SH ad Ellipseos diametrum AB; tum etiam longitudo quædam L, quæ sit ad radium in eadem ratione inverse. Quibus semel inventis, Problema deinceps confit per sequentem Analysin. Per constructionem superiorem (vel utcunq; conjecturam faciendo) cognoscatur corporis locus P quam proxime. Demissaq; ad axem Ellipseos ordinatim applicata PR, ex proportione diametrorum Ellipseos, dabitur circuli circumscripti AQB ordinatim applicata RQ, quæ sinus est anguli ACQ existente AC radio. Sufficit angulum illum rudi calculo in numeris proximis invenire. Cognoscatur etiam angulus tempori proportionalis, id est, qui sit ad quatuor rectos ut est tempus quo corpus descripsit arcum AP, ad tempus revolutionis unius in Ellipsi. Sit angulus iste N. Tum capiatur & angulus D ad angulum B, ut est sinus iste anguli ACQ ad Radium, & angulus E ad angulum N−ACQ+D, ut est longitudo L ad longitudinem eandem L cosinu anguli ACQ+ D diminutam, ubi angulus iste recto minor est, auctam ubi major. Postea capiatur tum angulus F ad angulum B, ut est sinus anguli ACQ+E ad radium, tum angulus G ad angulum N−ACQ−E+F ut est longitudo L ad Longitudinem eandem cosinu anguli ACQ+E+F diminutam ubi angulus iste recto minor est, auctam ubi major. Tertia vice capiatur angulus H ad angulum B, ut est sinus anguli ACQ+E+G ad radium; & angulus I ad angulum N−ACQ−E−G+H, ut est longitudo L ad eandem longitudinem cosinu anguli ACQ+E+G+H diminutam, ubi angulus iste recto minor est, auctam ubi major. Et sic pergere licet in infinitum. Deniq; capiatur angulus ACq æqualis angulo ACQ+E+G+I & c. & ex cosinu ejus Cr & ordinata pr, quæ est ab sinum qr ut Ellipseos axis minor ad axem majorem, habebitur corporis locus correctus p. Siquando angulus N−ACQ+D negativus est, debet signum+ipsius E ubiq; mutari in -, & signum - in +. Idem intelligendum est de signis ipsorum G & I, ubi anguli N−ACQ−E+F, & N−ACQ−E−G+H negative prodeunt. Convergit autem series infinita ACQ+E+G+I quam celerrime, adeo ut vix unquam opus fuerit ultra progredi quam ad terminum secundum E. Et fundatur calculus in hoc Theoremate, quod area APS sit ut differentia inter arcum AQ & rectam ab umbilico S in Radium CQ perpendiculariter demissam.

Non dissimili calculo conficitur Problema in Hyperbola. Sit ejus centrum C, Vertex A, Umbilicus S & Asymptotos CK. Cognoscatur quantitas areæ APS tempori proportionalis. Sit ea A, & fiat conjectura de positione rectæ SP, quæ aream illam abscindat quamproxime. Jungatur CP, & ab A & P ad Asymptoton agantur AI, PK Asymptoto alteri parallelæ, & per Tabulam Logarithmorum dabitur Area AIKP, eiq; æqualis area CPA, quæ subducta de triangulo CPS relinquet aream APS. Applicando arearum A & APS semidifferentiam APS−A vel A− APS ad lineam SN, quæ ab umbilico S in tangentem PT perpendicularis est, orietur longitudo PQ. Capiatur autem PQ inter A & P, si area APS major sit area A, secus ad puncti P contrarias partes: & punctum Q erit locus corporis accuratius. Et computatione repetita invenietur idem accuratius in perpetuum.
Atq; his calculis Problema generaliter confit Analytice. Verum usibus Astronomicis accommodatior est calculus particularis qui sequitur. Existentibus AO, OB, OD semiaxibus Ellipseos, (Vide fig. pag. 74.) & L ipsius latere recto, quære tum angulum Y, cujus Tangens sit ad Radium ut est semiaxium differentia AO−OD ad eorum summam AO+OD; tum angulum Z, cujus tangens sit ad Radium ut rectangulum sub umbilicorum distantia SH & semiaxium differentia AO−OD ad triplum rectangulum sub OQ semiaxe minore & AO−L differentia inter semiaxem majorem & quartam partem lateris recti. His angulis semel inventis, locus corporis sic deinceps determinabitur. Sume angulum T proportionalem tempori quo arcus BP descriptus est, seu motui medio (ut loquuntur) æqualem; & angulum V (primam medii motus æquationem) ad angulum Y (æquationem maximam primam) ut est sinus anguli T duplicati ad radium; atq; angulum X (æquationem secundam) ad angulum Z (æquationem maximam secundam) ut est sinus versus anguli T duplicati ad radium duplicatum, vel (quod eodem recidit) ut est quadratum sinus anguli T ad quadratum Radii. Angulorum T, V, X vel summæ T+X+V, si angulus T recto minor est, vel differentiæ T+X−V, si is recto major est rectisq; duobus minor, æqualem cape angulum BHP (motum medium æquatum;) & si HP occurrat Ellipsi in P, acta SP abscindet aream BSP tempori proportionalem quamproxime. Hæc Praxis satis expedita videtur, propterea quod angulorum perexiguorum V & X (in minutis secundis, si placet, positorum) figuras duas tresve primas invenire sufficit. Invento autem angulo motus medii æquati BHP, angulus veri motus HSP & distantia SP in promptu sunt per methodum notissimam Dris. Sethi Wardi Episcopi Salisburiensis mihi plurimum colendi.
Hactenus de motu corporum in lineis curvis. Fieri autem potest ut mobile recta descendat vel recta ascendat, & quæ ad istiusmodi motus spectant, pergo jam exponere.










