Scholium.
Nomen Conicæ sectionis in hoc Lemmate late sumitur, ita ut sectio tam rectilinea per verticem Coni transiens, quam circularis basi parallela includatur. Nam si punctum p incidit in rectam, qua quævis ex punctis quatuor A, B, C, D junguntur, Conica sectio vertetur in geminas rectas, quarum una est recta illa in quam punctum p incidit, & altera recta qua alia duo ex punctis quatuor junguntur. Si trapezii anguli duo oppositi simul sumpti æquentur duobus rectis, & lineæ quatuor PQ, PR, PS, PT ducantur ad latera ejus vel perpendiculariter vel in angulis quibusvis æqualibus, sitq; rectangulum sub duabus ductis PS×PR æquale rectangulo sub duabus aliis PS×PT, Sectio conica evadet Circulus. Idem fiet si lineæ quatuor ducantur in angulis quibusvis & rectangulum sub duabus ductis PQ×PR sit ad rectangulum sub aliis duabus PS×PT ut rectangulum sub sinubus angulorum S, T, in quibus duæ ultimæ PS, PT ducuntur, ad rectangulum sub sinubus angulorum Q, R, in quibus duæ primæ PQ, PR ducuntur. Cæteris in casibus Locus puncti P erit aliqua trium figurarum quæ vulgo nominantur Sectiones Conicæ. Vice autem Trapezii ABCD substitui potest quadrilaterum cujus latera duo opposita se mutuo instar diagonalium decussant. Sed & e punctis quatuor A, B, C, D possunt unum vel duo abire in infinitum, eoq; pacto latera figuræ quæ ad puncta illa convergunt, evadere parallela: quo in casu sectio conica transibit per cætera puncta, & in plagas parallelarum abibit in infinitum.
Lemma XIX.
Invenire punctum P, a quo si rectæ quatuor PQ, PR, PS, PT ad alias totidem positione datas rectas AB, CD, AC, BD singulæ ad singulas in datis angulis ducantur, rectangulum sub duabus ductis, PQ×PR, sit ad rectangulum sub aliis duabus, PS×PT, in data ratione.
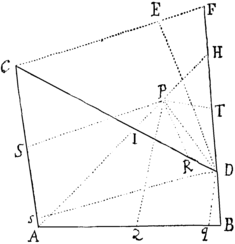
Lineæ AB, CD, ad quas rectæ duæ PQ, PR, unum rectangulorum continentes ducuntur, conveniant cum aliis duabus positione datis lineis in punctis A, B, C, D. Ab eorum aliquo A age rectam quamlibet AH, in qua velis punctum P reperiri. Secet ea lineas oppositas BD, CD, nimirum BD in H & CD in I, & ob datos omnes angulos figuræ, dabuntur rationes PQ ad PA & PA ad PS, adeoq; ratio PQ ad PS. Auferendo hanc adata ratione PQ×PR ad PS×PT, dabitur ratio PR ad PT, & addendo datas rationes PI ad PR, & PT ad PH dabitur ratio PI ad PH atq; adeo punctum P. Q. E. I.
Corol. 1. Hinc etiam ad Loci punctorum infinitorum P punctum quodvis D tangens duci potest. Nam chorda PD ubi puncta P ac D conveniunt, hoc est, ubi AH ducitur per punctum D, tangens evadit. Quo in casu, ultima ratio evanescentium IP & PH invenietur ut supra. Ipsi igitur AD duc parallelam CF, occurrentem BD in F, & in ea ultima ratione sectam in E, & DE tangens

