| SECT. III. De motu corporum quæ resistuntur partim in ratione velocitatis, partim in ejusdem ratione duplicata. |
|
SECT. II.
De motu corporum quibus resistitur in duplicata ratione velocitatum.
Prop. V. Theor. III.
Si corpori resistitur in velocitatis ratione duplicata, & sola vi insita per Medium similare movetur, tempora vero sumantur in progressione Geometrica a minoribus terminis ad majores pergente: dico quod velocitates initio singulorum temporum sunt in eadem progressione Geometrica inverse, & quod spatia sunt æqualia quæ singulis temporibus describuntur.
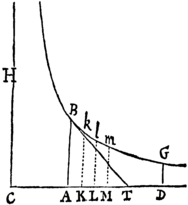
Nam quoniam quadrato velocitatis proportionalis est resistentia Medii, & resistentiæ proportionale est decrementum velocitatis; si tempus in particulas innumeras æquales dividatur, quadrata velocitatum singulis temporum initiis erunt velocitatum earundem differentiis proportionalia. Sunto temporis particulæ illæ AK, KL, LM , &c. in recta CD sumptæ, & erigantur perpendicula AB, Kk, Ll, M m, &c. Hyperbolæ BklmG, centro C Asymptotis rectangulis CD, CH descriptæ occurrentia in B, k, l, m, &c. & erit AB ad Kk ut CK ad CA, & divisim AB−Kk ad Kk ut AK ad CA, & vicissim AB−Kk ad AK ut Kk ad CA, adeoq; ut AB×Kk ad AB×CA. Unde cum AK & AB×CA dentur, erit AB−Kk ut AB×Kk; & ultimo, ubi coeunt AB & Kk, ut ABq. Et simili argumento erunt Kk−Ll, Ll−Mm, &c. ut Kkq., Llq. &c. Linearum igitur AB, Kk, Ll, Mm quadrata sunt ut earundem differentiæ, & idcirco cum quadrata velocitatum fuerint etiam ut ipsarum differentiæ, similis erit ambarum progressio. Quo demonstrato, consequens est etiam ut areæ his lineis descriptæ sint in progressione consimili cum spatiis quæ velocitatibus describuntur. Ergo si velocitas initio primi temporis AK exponatur per lineam AB, & velocitas initio secundi KL per lineam Kk, & longitudo primo tempore descripta per arcam AKkB, velocitates omnes subsequentes exponentur per lineas subsequentes Ll, Mm, &c. & longitudines descriptæ per areas Kl, Lm, &c. & composite, si tempus totum exponatur per summam partium suarum AM, longitudo tota descripta exponetur per summam partium suarum AM mB. Concipe jam tempus AM ita dividi in partes AK, KL, LM, &c. ut sint CA, CK, CL, CM, &c. in progressione Geometrica, & erunt partes illæ in eadem progressione, & velocitates AB, Kk, Ll, M m, &c. in progressione eadem inversa, atq; spatia descripta Ak, Kl, Lm, &c. æqualia. Q. E. D.
Corol. 1. Patet ergo quod si tempus exponatur per Asymptoti partem quamvis AD, & velocitas in principio temporis per ordinatim applicatam AB; velocitas in fine temporis exponetur per ordinatam DG, & spatium totum descriptum per aream Hyperbolicam adjacentem ABGD; necnon spatium quod corpus aliquod eodem tempore AD, velocitate prima AB in Medio non resistente describere posset, per rectangulum AB×AD.
Corol. 2. Unde datur spatium in Medio resistente descriptum, capiendo illud ad spatium quod velocitate uniformi AB in Medio non resistente simul describi posset, ut est area Hyperbolica ABGD ad rectangulum AB×AD.
Corol. 3. Datur etiam resistentia Medii, statuendo eam ipso motus initio æqualem esse vi uniformi centripetæ, quæ, in cadente corpore, tempore AC, in Medio non resistente, generare posset velocitatem AB. Nam si ducatur BT quæ tangat Hyperbolam in B, & occurrat Asymptoto in T; recta AT æqualis erit ipsi AC, & tempus exponet quo resistentia prima uniformiter continuata tollere posset velocitatem totam AB.
Corol. 4. Et inde datur etiam proportio hujus resistentiæ ad vim gravitatis, aliamve quamvis datam vim centripetam.
Corol. 5. Et viceversa, si datur proportio resistentiæ ad datam quamvis vim centripetam, datur tempus AC, quo vis centripeta resistentiæ æqualis generare possit velocitatem quamvis AB; & inde datur punctum B per quod Hyperbola Asymptotis CH, CD describi debet; ut & spatium ABGD, quod corpus incipiendo motum suum cum velocitate illa AB, tempore quovis AD, in Medio similari resistente describere potest.
Prop. VI. Theor. IV.
Corpora Sphærica homogenea & æqualia, resistentiis in duplicata ratione velocitatum impedita, & solis viribus insitis incitata, temporibus quæ sunt reciproce ut velocitates sub initio, describunt semper æqualia spatia, & amittunt partes velocitatum proportionales totis.

Asymptotis rectangulis CD, CH descripta Hyperbola quavis BbEe secante perpendicula AB, ab, DE, de, in B, b, E, e, exponantur velocitates initiales per perpendicula AB, DE, & tempora per lineas Aa, Dd. Est ergo ut Aa ad Dd ita (per Hypothesin) DE ad AB, & ita (ex natura Hyperbolæ) CA ad CD; & componendo, ita Ca ad Cd. Ergo areæ ABba, DEed, hoc est spatia descripta æquantur inter se, & velocitates primæ AB, DE sunt ultimis ab, de, & propterea (dividendo) partibus etiam suis amissis AB−ab, DE−de proportionales. Q. E. D.
Prop. VII. Theor. V.
Corpora Sphærica quibus resistitur in duplicata ratione velocitatum, temporibus quæ sunt ut motus primi directe & resistentiæ primæ inverse, amittent partes motuum proportionales totis, & spatia describent temporibus istis in velocitates primas ductis proportionalia. Namq; motuum partes amissæ sunt ut resistentiæ & tempora conjunctim. Igitur ut partes illæ sint totis proportionales, debebit resistentia & tempus conjunctim esse ut motus. Proinde tempus erit ut Motus directe & resistentia inverse. Quare temporum particulis in ea ratione sumptis, corpora amittent semper particulas motuum proportionales totis, adeoq; retinebunt velocitates in ratione prima. Et ob datam velocitatum rationem, describent semper spatia quæ sunt ut velocitates primæ & tempora conjunctim. Q. E. D.
Corol. 1. Igitur si æquivelocia corpora resistuntur in duplicata ratione diametrorum, Globi homogenei quibuscunq; cum velocitatibus moti, describendo spatia diametris suis proportionalia, amittent partes motuum proportionales totis. Motus enim Globi cujusq; erit ut ejus velocitas & Massa conjunctim, id est ut velocitas & cubus diametri; resistentia (per Hypothesin) erit ut quadratum diametri & quadratum velocitatis conjunctim; & tempus (per hanc Propositionem) est in ratione priore directe & ratione posteriore inverse, id est ut diameter directe & velocitas inverse; adeoq; spatium (tempori & velocitati proportionale) est ut diameter.
Corol. 2. Si æquivelocia corpora resistuntur in ratione sesquialtera diametrorum: Globi homogenei quibuscunq; cum velocitatibus moti, describendo spatia in sesquialtera ratione diametrorum inverse, amittent partes motuum proportionales totis. Nam tempus augetur in ratione resistentiæ diminutæ, & spatium augetur in ratione temporis.
Corol. 3. Et universaliter, si æquivelocia corpora resistuntur in ratione dignitatis cujuscunq; diametrorum, spatia quibus Globi homogenei, quibuscunq; cum velocitatibus moti, amittent partes motuum proportionales totis, erunt ut cubi diametrorum ad dignitatem illam applicata. Sunto diametri D & E; & si resistentiæ sint ut Dn & En, spatia quibus amittent partes motuum proportionales totis, erunt ut D3−n & E3−n. Igitur describendo spatia ipsis D3−n & E3−n proportionalia, retinebunt velocitates in eadem ratione ad invicem ac sub initio.
Corol. 4. Quod si Globi non sint homogenei, spatium a Globo densiore descriptum augeri debet in ratione densitatis. Motus enim sub pari velocitate major est in ratione densitatis, & tempus (per hanc Propositionem) augetur in ratione motus directe, ac spatium descriptum in ratione temporis.
Corol. 5. Et si Globi moveantur in Mediis diversis, spatium in Medio, quod cæteris paribus magis resistit, diminuendum erit in ratione majoris resistentiæ. Tempus enim (per hanc Propositionem) diminuetur in ratione resistentiæ, & spatium in ratione temporis.
Lemma II.
Momentum Genitæ æquatur momentis Terminorum singulorum generantium in eorundem laterum indices dignitatum & coefficientia continue ductis.
Genitam voco quantitatem omnem quæ ex Terminis quibuscunq; in Arithmetica per multiplicationem, divisionem, & extractionem radicum; in Geometria per inventionem vel contentorum & laterum, vel extremarum & mediarum proportionalium absq; additione & subductione generatur. Ejusmodi quantitates sunt Facti, Quoti, Radices, rectangula, quadrata, cubi, latera quadrata, latera cubica & similes. Has quantitates ut indeterminatas & instabiles, & quasi motu fluxuve perpetuo crescentes vel decrescentes hic considero, & eorum incrementa vel decrementa momentanea sub nomine momentorum intelligo: ita ut incrementa pro momentis addititiis seu affirmativis, ac decrementa pro subductitiis seu negativis habeantur. Cave tamen intellexeris particulas finitas. Momenta, quam primum finitæ sunt magnitudinis, desinunt esse momenta. Finiri enim repugnat aliquatenus perpetuo eorum incremento vel decremento. Intelligenda sunt principia jamjam nascentia finitarum magnitudinum. Neq; enim spectatur in hoc Lemmate magnitudo momentorum, sed prima nascentium proportio. Eodem recidit si loco momentorum usurpentur vel velocitates incrementorum ac decrementorum, (quas etiam motus, mutationes & fluxiones quantitatum nom inare licet) vel finitæ quævis quantitates velocitatibus hisce proportionales. Termini autem cujusq; Generantis coefficiens est quantitas, quæ oritur applicando Genitam ad hunc Terminum.
Igitur sensus Lemmatis est, ut si quantitatum quarumcunq; perpetuo motu crescentium vel decrescentium A, B, C, &c. Momenta, vel mutationum velocitates dicantur a, b, c, &c. momentum vel mutatio rectanguli AB fuerit Ab + aB, & contenti ABC momentum fuerit ABc+AbC+aBC: & dignita tum A2, A3, A4, A1/2, A3/2, A1/3, A2/3, , , & momenta 2Aa, 3aA2, 4aA3, aA-1/2, aA1/2, aA-2/3, aA1/3, -aA-2, -2aA-3, & aA-3/2 respective. Et generaliter ut dignitatis cujuscunq; An/m momentum fuerit . Item ut Genitæ Aquad.×B momentum fuerit 2aAB+A2b; & Genitæ A3B4C2 momentum 3aA2B4C2+4A3bB3C2+2A3B4Cc; & Genitæ A3B2 sive A3B-2 momentum 3aA2B-2-2A3bB-3: & sic in cæteris. Demonstratur vero Lemma in hunc modum.
Cas. 1. Rectangulum quodvis motu perpetuo auctum AB, ubi de lateribus A & B deerant momentorum dimidia a & b, fuit A-a in B-b, seu AB-aB-Ab+ab; & quam primum latera A & B alteris momentorum dimidiis aucta sunt, evadit A+a in B+b seu AB+aB+Ab+ab. De hoc rectangulo subducatur rectangulum prius, & manebit excessus aB+Ab. Igitur laterum incrementis totis a & b generatur rectanguli incrementum aB+Ab. Q.E.D.
Cas. 2. Ponatur AB æquale G, & contenti ABC seu GC momentum (per Cas. 1.) erit gC+Gc, id est (si pro G & g scribantur AB & aB+Ab) aBC+ AbC+ABc. Et par est ratio contenti sub lateribus quotcunq;. Q. E. D.
Cas. 3. Ponantur A, B, C æqualia; & ipsius A2, id est rectanguli AB, momentum aB+Ab erit 2aA, ipsius autem A3, id est contenti ABC, momen tum aBC+AbC+ABc erit 3aA2. Et eodem argumento momentum dignitatis cujuscunq; An est naAn−1. Q. E. D.
Cas. 4. Unde cum in A sit 1, momentum ipsius ductum in A, una cum ducto in a erit momentum ipsius 1, id est nihil. Proinde momentum ipsius seu A-1 est . Et generaliter cum in An sit 1, momentum ipsius ductum in An una cum in naAn-1 erit nihil. Et propterea momentum ipsius seu A-n erit . Q.E.D. Cas. 5. Et cum A1/2 in A1/2 sit A, momentum ipsius A1/2 in 2A1/2 erit a, per Cas. 3: ideoq; momentum ipsius A1/2 erit sive 2aA-1/2. Et generaliter si ponatur Am/n æqualem B, erit Am æquale Bn, ideoq; maAm-1 æquale nbBm-1, & maA-1 æquale nbB-1 seu , adeoq; æquale b, id est æquale momento ipsius Am/n. Q.E.D.
Cas. 6. Igitur Genitæ cujuscunq; AmBn momentum est momentum ipsius Am ductum in Bn, una cum momento ipsius Bn ducto in Am, id est maAm-1+nbBn-1; idq; sive dignitatum indices m & n sint integri numeri vel fracti, sive affirmativi vel negativi. Et par est ratio contenti sub pluribus dignitatibus. Q.E.D.
Corol. 1. Hinc in continue proportionalibus, si terminus unus datur, momenta terminorum reliquorum erunt ut iidem termini multiplicati per numerum intervallorum inter ipsos & terminum datum. Sunto A, B, C, D, E, F continue proportionales; & si detur terminus C, momenta reliquorum terminorum erunt inter se ut −2A, −B, D, 2E, 3F.
Corol. 2. Et si in quatuor proportionalibus duæ mediæ dentur, momenta extremarum erunt ut eædem extremæ. Idem intelligendum est de lateribus rectanguli cujuscunq; dati.
Corol. 3. Et si summa vel differentia duorum quadratorum detur, momenta laterum erunt reciproce ut latera.
Scholium.
In literis quæ mihi cum Geometra peritissimo G. G. Leibnitio annis abhinc decem intercedebant, cum significarem me compotem esse methodi determinandi Maximas & Minimas, ducendi Tangentes, & similia peragendi, quæ in terminis surdis æque ac in rationalibus procederet, & literis transpositis hanc sententiam involventibus [Data æquatione quotcunq; fluentes quantitates involvente, fluxiones invenire, & vice versa] eandem celarem: rescripsit Vir Clarissimus se quoq; in ejusmodi methodum incidisse, & methodum suam communicavit a mea vix abludentem præterquam in verborum & notarum formulis. Utriusq; fundamentum continetur in hoc Lemmate.
Prop. VIII. Theor. VI.
Si corpus in Medio uniformi, Gravitate uniformiter agente, recta ascendat vel descendat, & spatium totum descriptum distinguatur in partes æquales, inq; principiis singularum partium (addendo resistentiam Medii ad vim gravitatis, quando corpus ascendit, vel subducendo ipsam quando corpus descendit) colligantur vires absolutæ; dico quod vires illæ absolutæ sunt in progressione Geometrica.
Exponatur enim vis gravitatis per datam lineam AC; resistentia per lineam indefinitam AK; vis absoluta in descensu corporis per differentiam KC; velocitas corporis per lineam AP (quæ sit media proportionalis inter AK & AC,
ideoq; in dimidiata ratione resistentiæ) incrementum resistentiæ data temporis
particula factum per lineolam KL, & contemporaneum velocitatis incrementum per lineolam PQ; & centro C Asymptotis rectangulis CA, CH describatur Hyperbola quævis BNS, erectis perpendiculis AB, KN, LO, PR, QS occurrens in B, N, O, R, S. Quoniam AK est ut APq., erit hujus momentum KL ut illius momentum 2APQ, id est ut AP in KC. Nam velocitatis incrementum PQ, per motus Leg. 2. proportionale est vi generanti KC. Componatur ratio ipsius KL cum ratione ipsius KN, & fiet rectangulum KL×KN ut AP×KC×KN; hoc est, ob datum rectangulum KC×KN, ut AP. Atqui areæ Hyperbolicæ KNOL ad rectangulum KL×KN ratio ultima, ubi coeunt puncta K & L, est æqualitatis. Ergo area illa Hyperbolica evanescens est ut AP. Componitur igitur area tota Hyperbolica ABOL ex particulis KNOL velocitati AP semper proportionalibus, & propterea spatio velocitate ista descripto proportionalis est. Dividatur jam area illa in partes æquales ABMI, IMNK, KNOL, &c. & vires absolutæ AC, IC, KC, LC, &c. erunt in progressione Geometrica. Q. E. D.
Et simili argumento, in ascensu corporis, sumendo, ad contrariam partem puncti A, æquales areas ABmi, imnk, knol, &c. constabit quod vires absolutæ AC, iC, kC, lC, &c. sunt continue proportionales. Ideoq; si spatia omnia in ascensu & descensu capiantur æqualia; omnes vires absolutæ lC, kC, iC, AC, IC, KC, LC, &c. erunt continue proportionales. Q. E. D.
Corol. 1. Hinc si spatium descriptum exponatur per aream Hyperbolicam ABNK; exponi possunt vis gravitatis, velocitas corporis & resistentia Medii per lineas AC, AP & AK respective; & vice versa.
Corol. 2. Et velocitatis maximæ, quam corpus in infinitum descendendo potest unquam acquirere, exponens est linea AC.
Corol. 3. Igitur si in data aliqua velocitate cognoscatur resistentia Medii, invenietur velocitas maxima, sumendo ipsam ad velocitatem illam datam in dimidiata ratione, quam habet vis Gravitatis ad Medii resistentiam illam cognitam.
Corol. 4. Sed & particula temporis, quo spatii particula quam minima NKLO in descensu describitur, est ut rectangulum KN×PQ. Nam quoniam spatium NKLO est ut velocitas ducta in particulam temporis; erit particula temporis ut spatium illud applicatum ad velocitatem, id est ut rectangulum quam minimum KN×KL applicatum ad AP. Erat supra KL ut AP×PQ. Ergo particula temporis est ut KN×PQ, vel quod perinde est, ut . Q.E.D.
Corol. 5. Eodem argumento particula temporis, quo spatii particula nklo in ascensu describitur, est ut .
Prop. IX. Theor. VII.
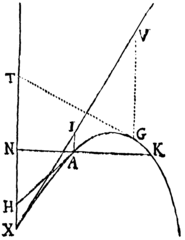
Positis jam demonstratis, dico quod si Tangentes angulorum sectoris Circularis & sectoris Hyperbolici sumantur velocitatibus proportionales, existente radio justæ magnitudinis: erit tempus omne ascensus futuri ut sector Circuli, & tempus omne descensus præteriti ut sector Hyperbolæ.
Rectæ AC, qua vis gravitatis exponitur, perpendicularis & æqualis ducatur AD. Centro D semidiametro AD describatur tum circuli Quadrans AtE, tum Hyperbola rectangula AVZ axem habens AX, verticem principalem A & Asymptoton DC. Jungantur Dp, DP, & erit sector circularis AtD ut tempus ascensus omnis futuri; & Sector Hyperbolicus ATD ut tempus descensus omnis præteriti, si modo Sectorem tangentes Ap & AP sint velocitates.

Cas. 1. Agatur enim Dvq abscindens Sectoris ADt & trianguli ADp momenta, seu particulas quam minimas simul descriptas tDv & pDq. Cum particulæ illæ, ob angulum communem D, sunt in duplicata ratione laterum, erit particula tDv ut . Sed pD quad. est AD quad. +Ap quad. id est AD quad.+Ak×AD seu AD×Ck; &qDp est AD×pq. Ergo Sectoris particula vDt est ut , id est, per Corol. 5, Prop. VIII. ut particula temporis. Et componendo fit summa particularum omnium tDv in Sectore ADt, ut summa particularum temporis singulis velocitatis decrescentis Ap particulis amissis pq respondentium, usq; dum velocitas illa in nihilum diminuta evanuerit; hoc est, Sector totus ADt est ut ascensus totius futuri tempus. Q. E. D.
Cas. 2. Agatur DQV abscindens tum Sectoris DAV, tum trianguli DAQ particulas quam minimas TDV & PDQ; & erunt hæ particulæ ad invicem ut DTq. ad DPq. id est (si TX & AP parallelæ sint) ut DXq. ad DAq. vel TXq. ad APq. & divisim ut DXq.−TXq. ad ADq.−APq. Sed ex natura Hyperbolæ DXq.−TXq. est ADq., & per Hypothesin APq. est AD×AK. Ergo particulæ sunt ad invicem ut ADq. ad ADq.−AD×AK; id est ut AD ad AD−AK seu AC ad CK: ideoq; Sectoris particula TDV est , atq; adeo ob datas AC & AD, ut ; & propterea per Corol. 5. Prop. VIII. Lib. II. ut particula temporis incremento velocitatis PQ respondens. Et componendo fit summa particularum temporis, quibus omnes velocitatis AP particulæ PQ generantur, ut summa particularum Sectoris ADT, id est tempus totum ut Sector totus. Q.E.D.
Corol. 1. Hinc si AB æquetur quartæ parti ipsius AC, spatium ABRP, quod corpus tempore quovis ATD cadendo describit, erit ad spatium quod corpus semisse velocitatis maximæ AC, eodem tempore uniformiter progrediendo describere potest, ut area ABRP, qua spatium cadendo descriptum exponitur, ad aream ATD qua tempus exponitur. Nam cum sit AC ad AP ut AP ad AK, erit 2APQ æquale AC×KL (per Corol. 1. Lem. II. hujus) adeoq; KL ad PQ ut 2AP ad AC, & inde LKN ad PQ×AD seu DPQ ut 2AP×KN ad AC×AD. Sed erat DPQ ad DTV ut CK ad AC. Ergo ex æquo LKN est ad DTV ut 2AP×KN×CK ad AC cub.; id est, ob æquales CKN & ACq., ut AP ad AC; hoc est ut velocitas corporis cadentis ad velocitatem maximam quam corpus cadendo potest acquirere. Cum igitur arearum ABKN & AVD momenta LKN & DTV sunt ut velocitates, erunt arearum illarum partes omnes simul genitæ ut spatia simul descripta, ideoq; areæ totæ ab initio genitæ ABKN & AVD ut spatia tota ab initio descensus descripta. Q. E. D.
Corol. 2. Idem consequitur etiam de spatio quod in ascensu describitur. Nimirum quod spatium illud omne sit ad spatium, uniformi cum velocitate AC eodem tempore descriptum, ut est area ABnk ad Sectorem ADt.
Corol. 3. Velocitas corporis tempore ATD cadentis est ad velocitatem, quam eodem tempore in spatio non resistente acquireret, ut triangulum APD ad Sectorem Hyperbolicum ATD. Nam velocitas in Medio non resistente foret ut tempus ATD, & in Medio resistente est ut AP, id est ut triangulum APD. Et velocitates illæ initio descensus æquantur inter se, perinde ut areæ illæ ATD, APD.
Corol. 4. Eodem argumento velocitas in ascensu est ad velocitatem, qua corpus eodem tempore in spatio non resistente omnem suum ascendendi motum amittere posset, ut triangulum ApD ad Sectorem circularem AtD, sive ut recta Ap ad arcum At.
Corol. 5. Est igitur tempus quo corpus in Medio resistente cadendo velocitatem AP acquirit, ad tempus quo velocitatem maximam AC in spatio non resistente cadendo acquirere posset, ut Sector ADT ad triangulum ADC: & tempus, quo velocitatem Ap in Medio resistente ascendendo possit amittere, ad tempus quo velocitatem eandem in spatio non resistente ascendendo posset amittere, ut arcus At ad ejus Tangentem Ap.
Corol. 6. Hinc ex dato tempore datur spatium ascensu vel descensu descriptum. Nam corporis in infinitum descendentis datur velocitas maxima, per Corol. 2. & 3. Theor. VI, Lib. II. indeq; datur & spatium quod semisse velocitatis illius dato tempore describi potest, & tempus quo corpus velocitatem illam in spatio non resistente cadendo posset acquirere. Et sumendo Sectorem ADT vel ADt ad triangulum ADC in ratione temporum; dabitur tum velocitas AP vel Ap, tum area ABKN vel ABkn, quæ est ad Sectorem ut spatium quæsitum ad spatium jam ante inventum.
Corol. 7. Et regrediendo, ex dato ascensus vel descensus spatio ABnk vel ABNK, dabitur tempus ADt vel ADT.
Prop. X. Prob. III.
Tendat uniformis vis gravitatis directe ad planum Horizontis, sitq; resistentia ut medii densitas & quadratum velocitatis conjunctim: requiritur tum Medii densitas in locis singulis, quæ faciat ut corpus in data quavis linea curva moveatur, tum corporis velocitas in iisdem locis.

Sit AK planum illud plano Schematis perpendiculare; ACK linea curva; C corpus in ipsa motum; & FCf recta ipsam tangens in C. Fingatur autem corpus C nunc progredi ab A ad K per lineam illam ACK, nunc vero regredi per eandem lineam; & in progressu impediri a Medio, in regressu æque promoveri, sic ut in iisdem locis eadem semper sit corporis progredientis & regredientis velocitas. Æqualibus autem temporibus describat corpus progrediens arcum quam minimum CG, & corpus regrediens arcum Cg; & sint CH, Ch longitudines æquales rectilineæ, quas corpora de loco C exeuntia, his temporibus, absq; Medii & Gravitatis actionibus describerent: & a punctis C, G, g, ad planum horizontale AK demittantur perpendicula CB, GD, gd, quorum GD ac gd tangenti occurrant in F & f. Per Medii resistentiam fit ut corpus progrediens, vice longitudinis CH, describat solummodo longitudinem CF ; & per vim gravitatis transfertur corpus de F in G: adeoq; lineola HF vi resistentiæ, & lineola FG vi gravitatis simul generantur. Proinde (per Lem. X. Lib. I.) lineola FG est ut vis gravitatis & quadratum temporis conjunctim, adeoq; (ob datam gravitatem) ut quadratum temporis; & lineola HF ut resistentia & quadratum temporis, hoc est ut resistentia & lineola FG. Et inde resistentia fit ut HF directe & FG inverse, sive ut . Hæc ita se habent in lineolis nascentibus. Nam in lineolis finitæ magnitudinis hæ rationes non sunt accuratæ.
Et simili argumento est fg ut quadratum temporis, adeoq; ob æqualia tempora æquatur ipsi FG; & impulsus quo corpus regrediens urgetur est ut . Sed impulsus corporis regredientis & resistentia progredientis ipso motus initio æquantur, adeoq; & ipsis proportionales & æquantur; & propterea ob æquales fg & FG, æquantur etiam hf & HF, suntq; adeo CF, CH (vel Ch) & Cf in progressione Arithmetica, & inde HF semidifferentia est ipsarum Cf & CF; & resistentia quæ supra fuit ut , est ut .
Est autem resistentia ut Medii densitas & quadratum velocitatis. Veloci tas autem ut descripta longitudo CF directe & tempus √FG inverse, hoc est ut CF √FG, adeoq; quadratum velocitatis ut . Quare resistentia, ipsiq; pro portionalis est ut Medii densitas & ut conjunctim; & inde Medii densitas ut directe & inverse, id est ut Q. E. I.
Corol. 1. Et hinc colligitur, quod si in Cf capiatur Ck æqualis CF, & ad planum horizontale AK demittatur perpendiculum ki, secans curvam ACK in l; fiet Medii densitas ut . Erit enimfC ad kC ut √fg seu √FG ad √kl,& divisim fk ad kC,id est Cf−CF ad CF ut √FG√kl ad √kl; hoc est (si ducatur terminus uterq; in √FG+√kl) ut FG−kl ad kl +√FG×kl, sive ad FG+kl. Nam ratioprima nascentium kl+√FG×kl & FG+kl est æqualitatis. Scribatur itaq; pro ; & Medii densitas, quæ fuit ut quad. evadet ut . Corol. 2. Unde cum 2HF & Cf−CF æquentur, & FG & kl (ob rationem æqualitatis) componant 2FG; erit 2HF ad CF ut FG−kl ad 2FG; et inde HF ad FG, hoc est resistentia ad gravitatem, ut rectangulum CF in FG−kl ad 4FG quad.
Corol. 3. Et hinc si curva linea definiatur per relationem inter basem seu abscissam AB & ordinatim applicatam BC; (ut moris est) & valor ordina tim applicatæ resolvatur in seriem convergentem: Problema per primos seriei terminos expedite solvetur: ut in Exemplis sequentibus.
Exempl. 1. Sit Linea ACK semicirculus super diametro AK descriptus, & requiratur Medii densitas quæ faciat ut Projectile in hac linea moveatur. Bisecetur semicirculi diameter AK in O; & dic OKn, OBa, BCe, & BD vel Bio: & erit DGq. seu OGq.−ODq. æquale nn−aa−2ao−oo seu ee−2ao−oo; & radice per methodum nostram extracta, fiet &c. Hic scribatur nnpro ee+aa & evadet &c.
Hujusmodi Series distinguo in terminos successivos in hunc modum. Terminum primum appello in quo quantitas infinite parva o non extat; secundum in quo quantitas illa extat unius dimensionis; tertium in quo extat duarum, quartum in quo trium est, & sic in infinitum. Et primus terminus, qui hic est e, denotabit semper longitudinem ordinatæ BC insistentis ad indefinitæ quantitatis initium B; secundus terminus qui hic est , denotabit differentiam inter BC & DF, id est lineolam IF, quæ abscinditur complendo parallelogrammum BC−ID, atq; adeo positionem Tangentis CF semper determinat: ut in hoc casu capiendo IF ad IC ut est ad o seu a ad e. Terminus tertius, qui hic est designabit lineolam FG, quæ jacet inter Tangentem & Curvam, adeoq; determinat angulum contactus FCG, seu curvaturam quam curva linea habet in C. Si lineola illa FG finitæ est magnitudinis, designabitur per terminum tertium una cum subsequentibus in infinitum. At si lineola illa minuatur in infinitum, termini subsequentes evadent infinite minores tertio, ideoq; negligi possunt. Terminus quartus, qui hic est , exhibet variationem Curvaturæ; quintus variationem variationis, & sic deinceps. Unde obiter patet usus non contemnendus harum Serierum in solutione Problematum, quæ pendent a Tangentibus & curvatura Curvarum.
Præterea CF est latus quadratum ex CIq. & IFq. hoc est ex BDq. & quadra to termini secundi. Estq; FG+kl æqualis duplo termini tertii, & FG−kl æqualis duplo quarti. Nam valor ipsius DG convertitur in valorem ipsius il, & valor ipsius FG in valorem ipsius kl, scribendo Bi pro BD, seu −o pro +o. Proinde cum FG sit &c. erit , &c. Et horum summa est , differentia . Terminum quintum & sequentes hic negligo, ut infinite minores quam qui in hoc Problemate considerandi veniant. Itaq; si designetur Series universaliter his terminis &c. erit CF æqualis √oo+QQoo, FG+kl æqualis 2Roo, & FG−kl æqualis . Pro CF, FG+kl & FG−kl scribantur hi earum valores, & Medii densitas quæ erat ut in FG+kl jamfiet ut . Deducendo igitur Problema unumquodq; ad seriem convergentem, & hic pro Q, R & S scribendo terminos seriei ipsis respondentes; deinde etiam ponendo resistentiam Medii in loco quovis G esse ad Gravitatem ut ad 2RR, & velocitatem esse illam ipsam quacum corpus, de loco C secundum rectam CF egrediens, in Parabola, diametrum CB & latus rectum habente, deinceps moveri posset, solvetur Problema.
Sic in Problemate jam solvendo, si scribantur seun e pro √1+QQ, pro R, & pro S, prodibit Medii densitas ut a ne, hoc est (obdatam n) ut seu , id est ut Tangentis longitudo illa CT, quæ ad semidiametrum OL ipsi AK normaliter insistentem terminatur, & resistentia erit ad gravitatem ut a ad n, id est ut OB ad circuli semidiametrum OK, velocitas autem erit ut √2BC. Igitur si corpus C certa cum velocitate, secundum lineam ipsi OK parallelam, exeat de loco L, & Medii densitas in singulis locis C sit ut longitudo tangentis CT, & resistentia etiam in loco aliquo C sit ad vim gravitatis ut OB ad OK; corpus illud describet circuli quadrantem LCK. Q. E. I.
At si corpus idem de loco A secundum lineam ipsi AK perpendicularem egrederetur, sumenda esset OB seu a ad contrarias partes centri O, & propterea signum ejus mutandum esset, & scribendum −a pro +a. Quo pacto prodiret Medii densitas ut . Negativam autem densitatem (hoc est quæ motus cor porum accelerat) Natura non admittit, & propterea naturaliter fieri non potest ut corpus ascendendo ab A describat circuli quadrantem AL. Ad hunc effectum deberet corpus a Medio impellente accelerari, non a resistente impediri.
Exempl. 2. Sit linea ALCK Parabola, axem habens OL horizonti AK perpendicularem, & requiratur Medii densitas quæ faciat ut projectile in ipsa moveatur.
Ex natura Parabolæ, rectangulum ADK æquale est rectangulo sub ordinata DG & recta aliqua data: hoc est, si dicantur recta illa b, ABa, AKc, BCe & BDo; rectangulum a+o in c−a−o seu ac−aa−2ao+co−oo æquale estrect angulo b in DG, adeoq; DG æquale . Jam scribendus esset hujus seriei secundus terminus pro Qo, & ejus coefficiens pro Q; tertius item terminus pro Roo, & ejus coefficiens pro R. Cum vero plures non sint termini, debebit quarti termini coefficiens S evanescere, & propterea quantitas cui Medii densitas proportionalis est, nihil erit. Nulla igitur Medii densitate movebitur Projectile in Parabola, uti olim demonstravit Galilæus. Q. E. I. Exempl. 3. Sit linea AGK Hyperbola, Asymptoton habens NX plano horizontali AK perpendicularem; & quæratur Medii densitas quæ faciat ut Projectile moveatur in hac linea.

Sit MX Asymptotos altera, ordinatim applicatæ DG productæ occurrens in V, & ex natura Hyperbolæ, rectangulum XV in VG dabitur. Datur autem ratio DN ad VX, & propterea datur etiam rectangulum DN in VG. Sit illud bb; & completo parallelogrammo DNXZ, dicatur BNa, BDo, NXc, & ratio data VZ ad ZX vel DN ponatur esse . Et erit DN æqualisa −o, VG æqualis , VZ æqualis , & GD seu NX−VZ−VG æqualis . Resolvatur terminus in seriem convergentem etc. & fiet GD æqualis &c. Hujus seriei terminus secundus usurpandus est pro Qo, tertius cum signo mutato pro , & quartus cum signo etiam mutato pro , eorumq; coefficientes , & scribendæ sunt, in Regula superi ore, pro Q, R & S. Quo facto prodit medii densitas ut seu
est, si in VZ sumatur VY æqualis VG, ut . Namq; aa & sunt ipsarum XZ & ZY quadrata. Resistentia autem invenitur in ratione ad Gravitatem quam habet XY ad YG, & velocitas ea est quacum corpus in Parabola pergeret verticem G diametrum DG & latus rectum YX quad. VG habente. Ponatur itaq; quod Medii densitates in locis singulis G sint reciproce ut distantiæ XY, quodq; resistentia in loco aliquo G sit ad gravitatem ut XY ad YG; & corpus de loco A justa cum velocitate emissum describet Hyperbolam illam AGK. Q. E. I.
Exempl. 4. Ponatur indefinite, quod linea AGK Hyperbola sit, centro X Asymptotis MX, NX, ea lege descripta, ut constructo rectangulo XZDN cujus latus ZD secet Hyperbolam in G & Asymptoton ejus in V, fuerit VG reciproce ut ipsius ZX vel DN dignitas aliqua NDn, cujus index est numerus n: & quæratur Medii densitas, qua Projectile progrediatur in hac curva. Pro DN, BD, NX scribantur A, O, C respective, sitq; VZ ad ZX vel DN ut d ad e, & VG æqualis , & erit DN æqualis A−O, , in A−O, & GD seu NX−VZ−VG æqualis . Resolvatur terminus ille in seriam infinitam &c. ac fiet GD æqualis +- &c. Hujus seriei terminus secundus - usurpandus est +pro Qo, tertius pro , quartus pro . Et inde Medii densitas , in loco quovis G, fit , adeoq; si in VZ capiatur VY æqualis n×VG, est reciproce ut XY. Sunt enim & in ipsarum XZ & ZY quadrata. Resistentia autem in eodem loco G fit ad Gravitatem ut S in ad 2RR, id est XY ad . Et velocitas ibidem ea ipsa est quacum corpus projectum in Parabola pergeret, verticem G, diametrum GD & Latus rectum seu habente. Q.E.I.
Scholium.
Quoniam motus non fit in Parabola nisi in Medio non resistente, in Hyperbolis vero hic descriptis fit per resistentiam perpetuam; perspicuum est quod linea, quam Projectile in Medio uniformiter resistente describit, propius accedit ad Hyperbolas hasce quam ad Parabolam. Est utiq; linea illa Hyperbolici generis, sed quæ circa verticem magis distat ab Asymptotis; in partibus a vertice remotioribus propius ad ipsas accedit quam pro ratione Hyperbolarum quas hic descripsi. Tanta vero non est inter has & illam differentia, quin illius loco possint hæ in rebus practicis non incommode adhiberi. Et utiliores forsan futuræ sunt hæ, quam Hyperbola magis accurata & simul magis composita. Ipsæ vero in usum sic deducentur.
Compleatur parallelogrammum XYGT, & ex natura harum Hyperbolarum facile colligitur quod recta GT tangit Hyperbolam in G, ideoq; densitas Medii in G est reciproce ut tangens GT, & velocitas ibidem ut , resistentia autem ad vim gravitatis ut GT ad .
Proinde si corpus de loco A secundum rectam AH projectum describat Hyperbolam AGK, & AH producta occurrat Asymptoto NX in H, actaq; AI occurrat alteri Asymptoto MX in I: erit Medii densitas in A reciproce ut AH, & corporis velocitas ut , ac resistentia ibidem ad Gravitatem ut AH ad in AI. Unde prodeunt sequentes Regulæ.
Reg. 1. Si servetur Medii densitas in A & mutetur angulus NAH, manebunt longitudines AH, AI, HX. Ideoq; si longitudines illæ in aliquo casu inveniantur, Hyperbola deinceps ex dato quovis angulo NAH expedite determinari potest. Reg. 2. Si servetur tum angulus NAH tum Medii densitas in A, & mutetur velocitas quacum corpus projicitur; servabitur longitudo AH, & mutabitur AI in duplicata ratione velocitatis reciproce.
Reg. 3. Si tam angulus NAH quam corporis velocitas in A, gravitasq; acceleratrix servetur, & proportio resistentiæ in A ad gravitatem motricem augeatur in ratione, quacunque: augebitur proportio AH ad AI eadem ratione, manente Parabolæ latere recto, eiq; proportionali longitudine ; & propterea minuetur AH in eadem ratione, & AI minuetur in ratione illa duplicata. Augetur vero proportio resistentiæ ad pondus, ubi vel gravitas specifica sub æquali magnitudine fit minor, vel Medii densitas major, vel resistentia, ex magnitudine diminuta, diminuitur in minore ratione quam pondus. Reg. 4. Quoniam densitas Medii prope verticem Hyperbolæ major est quam in loco A, ut servetur densitas mediocris, debet ratio minimæ tangentium GT ad Tangentem AH inveniri, & densitas in A, per Regulam tertiam, diminui in ratione paulo minore quam semisummæ Tangentium ad Tangentium AH.
Reg. 5. Si dantur longitudines AH, AI, & describenda sit figura AGK: pro duc HN ad X, ut sit HX æqualis facto sub n+1 & AI; centroq; X & Asymptotis MX, NX per punctum A describatur Hyperbola, ea lege ut sit AI ad quamvis VG ut ad .
Reg. 6. Quo major est numerus n, eo magis accuratæ sunt hæ Hyperbolæ in ascensu corporis ab A, & minus accuratæ in ejus descensu ad G; & contra. Hyperbola Conica mediocrem rationem tenet, estq; cæteris simplicior. Igitur si Hyperbola sit hujus generis, & punctum K, ubi corpus projectum incidet in rectam quamvis AN per punctum A transeuntem, quæratur: occurrat producta AN Asymptotis MX, NX in M & N, & sumatur NK ipsi AM æqualis.

Reg. 7. Et hinc liquet methodus expedita determinandi hanc Hyperbolam ex Phænomenis. Projiciantur corpora duo similia & æqualia eadem velocitate, in angulis diversis HAK, hAk, incidentq; in planum Horizontis in K & k; & notetur proportio AK ad Ak. Sit ea d ad e. Tum erecto cujusvis longitudinis perpendiculo AI, assume utcunq; longitudinem AH vel Ah, & inde collige graphice longitudines AK, Ak, per Reg. 6. Si ratio AK ad Ak sit eadem cum ratione d ad e, longitudo AH recte assumpta fuit. Sin minus cape in recta infinita SM longitudinem SM æqualem assumptæ AH, & erige perpendiculum MN æquale rationum differentiæ ductæ in rectam quamvis datam. Simili methodo ex assumptis pluribus longitudinibus AH invenienda sunt plura puncta N: & tum demum si per omnia agatur Curva linea regularis NNXN, hæc abscindet SX quæsitæ longitudini AH æqualem. Ad usus Mechanicos sufficit longitudines AH, AI easdem in angulis omnibus HAK retinere. Sin figura ad inveniendam resistentiam Medij accuratius determinanda sit, corrigendæ sunt
semper hæ longitudines per Regulam quartam.
Reg. 8. Inventis longitudinibus AH , HX; si jam desideretur positio rectæ AH , secundum quam Projectile data illa cum velocitate emissum incidit in punctum quodvis K: ad puncta A & K erigantur rectæ AC, KF horizonti perpendiculares, quarum AC deorsum tendat, & æquetur ipsi AI seu HX. Asymptotis AK, KF describatur Hyperbola, cujus Conjugata transeat per punctum C, centroq; A & intervallo AH describatur Circulus secans Hyperbo lam illam in puncto H ; & projectile secundum rectam AH emissum incidet in punctum K. Q. E. I. Nam punctum H, ob datam longitudinem AH, locatur alicubi in circulo descripto. Agatur CH occurrens ipsis AK & KF, illi in C, huic in F, & ob parallelas CH, MX & æquales AC, AI, erit AE æqualis AM, & propterea etiam æqualis KN. Sed CE est ad AE ut FH ad KN, & propterea CE & FH æquantur. Incidit ergo punctum H in Hyperbolam Asymptotis AK, KF descriptam, cujus conjugata transit per punctum C, atq; adeo reperitur in communi intersectione Hyperbolæ hujus & circuli descripti. Q. E. D. Notandum est autem quod hæc operatio perinde se habet, sive recta AKN horizonti parallela sit, sive ad horizontem in angulo quovis inclinata: quodq; ex duabus intersectionibus H, H duo prodeunt anguli NAH, NAH, quorum minor eligendus est; & quod in Praxi mechanica sufficit circulum semel describere, deinde regulam interminatam CH ita applicare ad punctum C, ut ejus pars FH, circulo & rectæ FK interjecta, æqualis sit ejus parti CE inter punctum C & rectam HK sitæ.
Quæ de Hyperbolis dicta sunt facile applicantur ad Parabolas. Nam si XAGK Parabolam designet quam recta XV tangat in vertice X, sintq; ordinatim applicatæ I A, VG ut quælibet abscissarum XI, XV dignitates ; agantur XT, TG, HA, quarum XT parallela sit VG, & TG, HA parabolam tangant in G & A: & corpus de loco quovis A, secundum rectam AH productam, justa cum velocitate projectum, describet hanc Parabolam, si modo densitas Medij, in locis singulis G, sit reciproce ut tangens GT. Velocitas autem in G ea erit quacum Projectile pergeret, in spatio non resistente, in Parabola Conica, verticem G, diametrum VG deorsum productam, & latus rectum habente. Et resistentia in G erit ad vim Gravitatis ut TG ad . Vnde si NAK lineam horizontalem designet, & manente tum densitate Medij in A, tum velocitate quacum corpus projicitur, mutetur utcunq; angulus NAH; manebunt longitudines AH, AI, HX, & inde datur Parabolæ vertex X, & positio rectæ XI, & sumendo VG ad IA ut ad , dantur omnia Parabolæ puncta G, per quæ Projectile transibit.









































































































